2021.05.30 - [이론공부/응용확률론] - 응용확률론 공부 #13 (베이즈 정리)
이전 내용
확률변수
- 취할 수 있는 모든 값에 대한 확률이 알려져 있는 변수
- 표본공간으로부터 실수값으로의 변환함수
- 표본공간 S에서의 함수
e.g) 두 주사위를 던졌을 대 나오는 눈의 합
이산 확률변수
- 확률변수가 취할 수 있는 값이 유한한 경우
연속 확률변수
- 확률변수가 취할 수 있는 값이 임의의 구간이나 구간들의 합으로 나타내는 경우
확률분포
- 확률의 결과를 시각적으로 표현한것
e.g 그래프, 표, 함수


확률 질량 함수


이산 누적분포함수





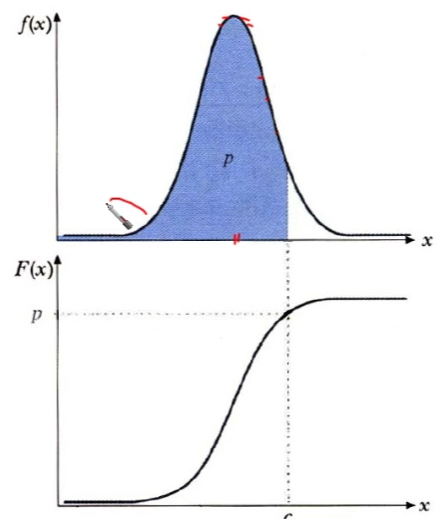
연속 확률분포


이산 확률질량함수는 그 값 자체가 확률 값을 의미 하지만, 연속 확률밀도함수는 그렇지 않다. 연속확률변수가 한 점을 취할 확률은 0 이다.
연속확률변수는 특정 구간에서의 확률만이 의미를 가지며, 그 확률은 그 구간에 대한 확률밀도함수의 면적으로 계산한다.

연속형 누적분포함수


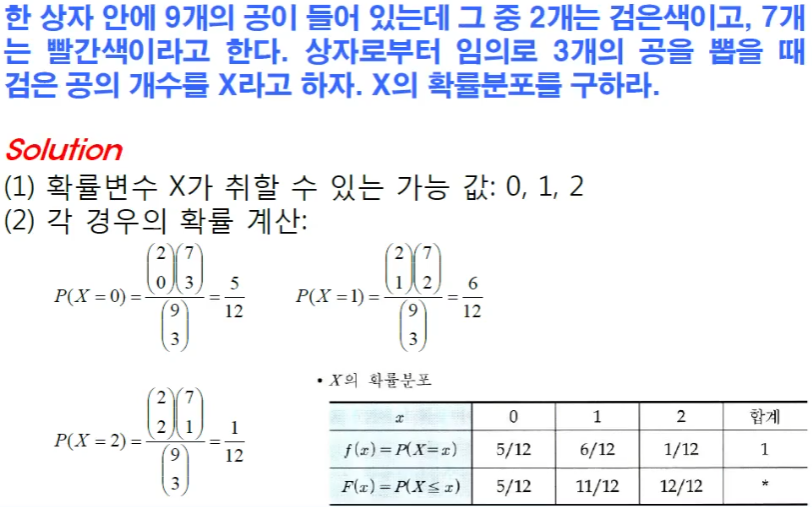
예제문제

'이론공부 > 응용확률론' 카테고리의 다른 글
| 응용확률론 공부 #16 (확률변수) (0) | 2021.06.30 |
|---|---|
| 응용확률론 공부 #15 (수학적 기대값) (0) | 2021.06.10 |
| 응용확률론 공부 #13 (베이즈 정리) (0) | 2021.05.30 |
| 응용확률론 공부 #12 (확률의 계산) (0) | 2021.05.13 |
| 응용확률론 공부 #11 (확률) (0) | 2021.04.22 |
