2021.05.04 - [이론공부/화일처리및응용] - 화일 처리 및 응용 공부 #12 (탐색 트리)
편향 이원 탐색 트리

트리의 높이가 제일 높은 구조이다 보니 리프노드의(25, 60) 탐색시간이 최악으로 될것이다.
이원 탐색 트리의 성능
성능
- 우수한 성능을 위해서 필요한 조건
- 가장 자주 접근되는 노드는 루투에 가장 가깝게 유지해야함
- 이원 탐색 트리를 균형 트리로 유지하는것이 좋음
- 만든 노드에 대해 양쪽 서브트리의 노드 수가 가능한 똑같게 만들어서 트리 높이를 최소로 한다.
단점
- 삽입, 삭제 이후 효율적 접근을 위한 균형 유지 부담이 큼
- 작은 분기율에 따른 긴 탐색 경로와 검색시간을 가짐
- 분기율이 2: 각 노드는 많아야 두개의 서브트리
- N개의 노드를 갖는 트리의 최소높이: [logN](소수점버림)+1
AVL 트리
- 삽입, 삭제, 검색 시간 : O(logN)
- 트리의 일부만 재균형시키면서 트리 전체가 균형을 계속 유지할 수 있도록 함
정의
- 각 노드의 왼쪽 서브트리의 높이와 오른쪽 서브트리의 높이 차이가 1 이하인 이원 탐색 트리
- |h(Left(N_i)) - h(Right(N_i))| ≤ 1. N_i ∈ T
- 공백 서브트리의 높이 : -1
균형인수
- 왼쪽 서브트리의 높이에서 오른쪽 서브트리의 높이를 뺀 값
- 노드의 균형 인수가
- ±1 이하이면 이 노드는 AVL 성질을 만족하고
- ±2 이상이면 이 노드는 AVL 성질을 만족하지않음
- AVL 트리의 모든 노드는 균형인수가 ±1 이하이다. 즉 AVL 트리의 모든 노드는 AVL 성질을 만족한다.

AVL 트리에서의 검색과 삽입
검색
- 일반 이원 트리와 검색 방법과 동일
- 시간 복잡도 : O(LogN)
삽입
- 삽입되는 노드에서부터 루트까지의 경로에 있는 부모 노드들의 균형인수에 영향이 있을 수 있음
- 노드 삽입으로 AVL 트리가 non_AVL 트리로 되면 삽입된 노드와 가장 가까우면서 불균형이 된 부모 노드의 균형 인수가 ±1 이하로 되게 트리 구조를 조정해야함.

AVL 트리가 삽입과정으로 인해 non_AVL 트리가 되었다. 이 성질을 유지하기 위해서는 non_AVL트리의 구조를 조정해야한다.


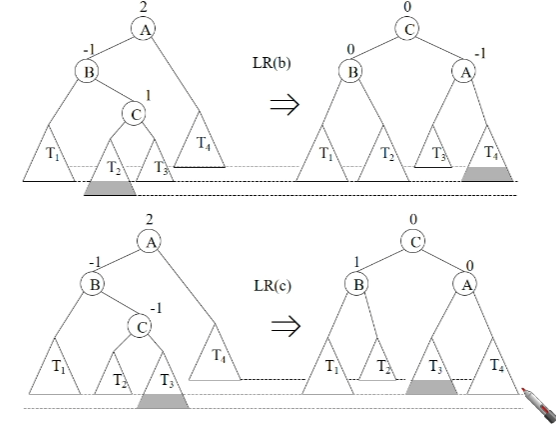
삽입 과정 요약

AVL 트리의 높이
- 높이 균형 이진 트리의 높이
- N개의 노드를 가진 높이 균형 이진 트리는 완전 균형 이진 트리보다 45%이상 높아지지 않음
- log(N+1)≤ 1.4404log(N+2)-0.328
- 높이 균형 이진 트리 대 완전 균형 이진 트리
- O(1.4 log N) 대 O(log N)
- 높이 균형 이진 트리의 탐색 시간이 더 길다
- 이유 : 트리 전체 재균형을 수행하지 않기 때문
- 수백만 개 노드로 구성된 AVL 트리가 디스크에 저장된 상태에서 노드의 탐색은 많은 횟수의 디스크 접근을 요구한다. 그래서 m-원 탐색 트리를 고려하게 된다.
m원 탐색 트리

- 트리의 노드가 m개 이하의 가지를 가질 수 있는 탐색 트리
- 이진 탐색 트리의 확장된 형태
- 탐색 트리의 제한을 따르고 2개 이상(m개 이하) 자식을 가질 수 있다
m원 탐색 트리의 분석
- m 원 탐색 트리의 탐색시간 : 탐색 경로 길이(높이)에 비례
- 각 레벨에서는 한 개의 노드만 탐색
- 분기율(m)을 높게 하면 트리의 높이가 낮아짐
- 한 노드에 m-1개 키 값을 저장하는 m원 탐색 트리
- 높이 h : n = (m^h-1)개 키값 저장
- ex) 4원 탑색 트리 : 높이가 3이면 n= (4^3-1) = 63개의 키 값을 저장
- n 개의 키를 가진 m원 탐색 트리
- 최소 높이 h = log_m (N+1)
- 최대 탐색 시간 : O(log_m(N+1))
ex) m=2 이면 : 이진 트리 탐색시간
3원 탐색 트리

느낀점 : 이전 내용을 잘 참고하고 자료구조때 배운 시간 복잡도 개념도 다시 확인하자
'이론공부 > 화일처리및응용' 카테고리의 다른 글
| 화일 처리 및 응용 공부 #15 (B*트리) (0) | 2021.05.27 |
|---|---|
| 화일 처리 및 응용 공부 #14 (B트리) (0) | 2021.05.26 |
| 화일 처리 및 응용 공부 #12 (탐색 트리) (0) | 2021.05.04 |
| 화일 처리 및 응용 공부 #11 (정렬/합병) (0) | 2021.04.20 |
| 화일 처리 및 응용 공부#10 (순차화일) (0) | 2021.03.30 |
