자료구조 공부#4 (순환, 반복)

2021.03.09 - [이론공부/자료구조] - 자료구조 공부#3 (알고리즘의 성능 분석)

이전 내용이 포함되어 있다. 이해가 안되는 부분이 있다면 이전 이론 공부 내용을 참고하길 바란다.
이전글과 마찬가지로 글속의 이미지 자료는 대부분 교수님이 수업도중 참고한 자료를 다시 가져온것이다.

순환(Recursion)

재귀호출(재귀함수), 되부름 이라는 단어로 많이 불린다.

알고리즘에서 함수가 수행도중 자기자신을 다시 호출하여 문제를 해결하는 기법이다.

정의 자체가 순환적으로 되어 있는경우에 사용하면 쉽게 해결이 가능하다

순환에서 팩토리얼의 정의

위와 같이 n!을 순환으로 정리 하면 아래와 같다.

int Factorial(int a){
	if(a <= 1) return(1);
    else return(a * Factorial(a - 1));
}

Factorial() 이라는 함수를 내부에서도 다시 호출하여 리턴값에 담아 이를 쌓아가면서 결과를 호출하는 방식이다.

만일, 위와같은 순환구조에서 호출을 하는부분만 존재하고 멈추는 부분이 존재하지 않는다면 시스템 오류(메모리 오버플로우, 스택 오버플로우) 가 발생한다.

이유를 설명하자면 리턴을 받는 과정에서 리턴을 받을 위치를 스택에 저장하게 되는데, 이게 용량이 유한적이여서 반복을 무한정 하게되면 결국 용량 부족으로 오버플로우가 일어나게 된다.

반복(Iteration)

반복문을 통하여 일정정해진 구간을 반복해서 문제를 해결하는 기법, 혹은 방식이라 한다.

대부분의 순환은 반복으로 바꾸어 작성할 수 있다.

반복에서 팩토리얼의 정의

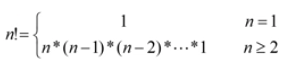
위와 같이 n!을 반복으로 구현 아면 아래의 코드를 예제로 들 수 있다.

int Factorial_2(int a){
	int b, c=1;
    for(b=a; b>0; b--)
    	c = c*b;
    retrurn(c);   
}

For 문을 통해서 계속 곱하는 과정을 a 만큼 반복하여 리턴값에 저장하여 결과를 도출하는 방식이다.

거듭제곱에서 순환, 반복 비교

거듭제곱 (x^n)을 구하는걸 요구할때, 순환적인 방법이 더 효율적이다.

반복에서의 알고리즘, 예제코드

Double Power_ITER(Double x, int n){
	int i;
    double result = 1.0;
	for(i=0; i<n; i++)
    	result = result * x;
    return(result);    
}
// 반복문의 경우

순환에서의 알고리즘

Power_RECUR(x,n)
if m==0 then return 1;
else if n이 짝수 then return Power_RECUR(x^2, n/2);
else if n이 홀수 then return x*Power_RECUR(x^2, (n-1)/2);

순환에서 예제 코드

double Power_RECUR(double x, int n){
	if (n==0) return 1;
    else if ((n%2==0)) return Power_RECUR(x^2,n/2);
    else return x* (Power_RECUR(x^2,(n-1)/2));
}

각각 기능으로서는 차이가 없지만 복잡도로서는 반복은 O(n), 순환은 O(logn)으로 순환이 제곱의 경우 좀더 효율적으로 문제를 해결 할 수 있다.

피보나치 수열에서 반복, 순환 비교

피보자치 수열 : 0,1, 1, 2, 3, 5, 8, 13, 21, 34, 55..........(이전값과 현재값을 더해서 다음값을 도출하는 수열)

피보나치 수열 순환식 코드 예제

int Fib(int n){
	if (n==0) return 0;
    	if (n==1) return 1;
    	return fib(n-1) + fib(n-2);
}

코드만 보면 3줄로 간결하고 효율적으로 보이지만, 매개변수를 크게 넣으면 넣을수록 불필요한 같은 과정을 중복해서 계산하게 된다.

이게 무슨 말이냐 하면 fib(5)를 계산 하는 경우 그 속에서 불필요하게 fib(3)을 두번 정도 더 계산하게 된다.

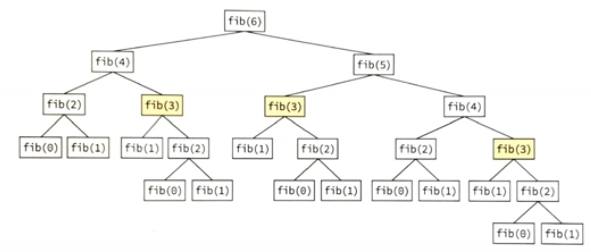
Fib(n)에서 n이 커질수록 중복 계산하는 항이더 많아질 것이고 이는 복잡도에 수직상승을 야기 해준다.

Fib(n) = Fib(n-1) + Fib(n-2) + C => O(2^n)

피보나치 수열 반복식 코드 예제

int Fib_Iter(int n){
	if(n==0) return 0;
    if(n==1) return 1;
    
    int pp = 0;
    int p = 1;
    int result = 0;
    
    for (int i=2; i<=n; i++){
    	result = p + pp;
        pp = p;
        p = result;    
    }
    return result;
}

순환에 반대로 반복을 통해서 해결하면 중복 과정이 없어져서 좀더 효율적으로 작동하게 될것이다.

느낀점 : 각각의 경우에따라 반복 순환으로 풀이할 수는 있지만, 그 효율성이 달라서 구현할떄 고민이 필요할것 같다. 수업 내용으로선 반복과 순환의 차이, 그 방식의 예를 아는것이 중요할 것이다.

한반가